上一章讲到Mesh的工作原理以及顶点与三角形的算法.本章主题如下:

  • Create a cube with a seamless mesh. 创建无缝Mesh的立方体
  • Add rounded edges to the cube. 添加圆形边缘的立方体

此为本人阅读笔记不作为转载处理,详细还请参看原文. 原文地址

Compositing a Cube 组合(方式)一个立方体

非重点,这里直接写实现思路.接上一章节生产面,只需修改每个面的角度位置.使其拼凑成为一个立方体即可.

使用六个面拼凑一个立方体

Creating Cube Vertices 创建立方体的顶点

计算所需定点数量

之前计算单个面的时候使用 (#x + 1)(#y + 1) 如下算法，那么可计算6个面的时候是不是可以直接套用单面的计算方式：2((#x + 1)(#y + 1) + (#x + 1)(#z + 1) + (#y + 1)(#z + 1)) 结论是否定的，其中角顶点与边顶点都被重复计算了。

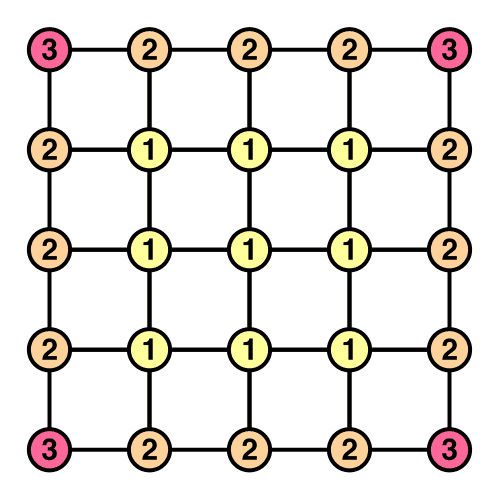
顶点被重复计算次数的用颜色区分

这其实也不是什么大问题。事实上顶点重复是非常常见的，譬如我们通常用网格创建锐角。所以我们可以创建6个面(的顶点)合并到单个数组里。
但是这不是我们打算做的，因为我们已经知道如何创建网格。我们的cube不需要有重复的顶点，这种做法很有趣。
我们需要多少顶点呢？让我们按类型分解，首先8个角顶点，这很简单。有12条边，每四条在同向。因为我们不包括角，每个边都有一个等于相应大小的顶点减去一个顶点。或者，把它看作四组x、y和z边。

4(#x + #y + #z - 3)

其余的顶点是那些位于面部边缘的顶点。这是相当于一个重复的顶点，其体积缩小了2

2((#x - 1)(#y - 1) + (#x - 1)(#z - 1) + (#y - 1)(#z - 1))

这样计算出的结果就是最终所需顶点数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private IEnumerator Generate () {
		GetComponent<MeshFilter>().mesh = mesh = new Mesh();
		mesh.name = "Procedural Cube";
		WaitForSeconds wait = new WaitForSeconds(0.05f);

		int cornerVertices = 8;
		int edgeVertices = (xSize + ySize + zSize - 3) * 4;
		int faceVertices = (
			(xSize - 1) * (ySize - 1) +
			(xSize - 1) * (zSize - 1) +
			(ySize - 1) * (zSize - 1)) * 2;
		vertices = new Vector3[cornerVertices + edgeVertices + faceVertices];

		yield return wait;
	}

现在定位一个面上的第一行顶点就像定位网格上的第一行顶点。(参考章节.1)
基础的算法是从x(0,0)开始，计算算一圈的点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int v = 0; //索引
//算出X轴线的点
for (int x = 0; x <= xSize; x++)
{
    Vertices[v++] = new Vector3(x, 0, 0);
    yield return wait;
}
//算出y轴线的点
for (int z = 1; z <= zSize; z++)
{
    Vertices[v++] = new Vector3(xSize, 0, z);
    yield return wait;
}
//x轴线背后的点
for (int x = (int)xSize - 1; x >= 0; x--)
{
    Vertices[v++] = new Vector3(x, 0, zSize);
    yield return wait;
}
//z轴线背后的点
for (int z = (int)zSize - 1; z > 0; z--)
{
    Vertices[v++] = new Vector3(0, 0, z);
    yield return wait;
}

由以上基础我们可以直接绘制出第0层至顶层的点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
int v = 0;
for (int y = 0; y <= ySize; y++)
{
    //算出X轴线的点
    for (int x = 0; x <= xSize; x++)
    {
        Vertices[v++] = new Vector3(x, y, 0);
        yield return wait;
    }
    //算出y轴线的点
    for (int z = 1; z <= zSize; z++)
    {
        Vertices[v++] = new Vector3(xSize, y, z);
        yield return wait;
    }
    //x轴线背后的点
    for (int x = (int)xSize - 1; x >= 0; x--)
    {
        Vertices[v++] = new Vector3(x, y, zSize);
        yield return wait;
    }
    //z轴线背后的点
    for (int z = (int)zSize - 1; z > 0; z--)
    {
        Vertices[v++] = new Vector3(0, y, z);
        yield return wait;
    }
}

//顶层内部的点
for (int z = 1; z < zSize; z++)
{
    for (int x = 1; x < xSize; x++)
    {
        Vertices[v++] = new Vector3(x, ySize, z);
        yield return wait;
    }
}
//底层内部的点
for (int z = 1; z < zSize; z++)
{
    for (int x = 1; x < xSize; x++)
    {
        Vertices[v++] = new Vector3(x, 0, z);
        yield return wait;
    }
}

Add rounded edges to the cube. 添加圆形边缘的立方体

和上一章类似，我们这样绘制四边形

1
2
3
4
5
6
7
8
private static int
SetQuad (int[] triangles, int i, int v00, int v10, int v01, int v11) {
    triangles[i] = v00;
    triangles[i + 1] = triangles[i + 4] = v01;
    triangles[i + 2] = triangles[i + 3] = v10;
    triangles[i + 5] = v11;
    return i + 6;
}

四边形图解

与顶点不同，三角形的数目等于六个面的总和。他们是否使用共享顶点并不重要。

1
2
3
4
5
private void CreateTriangles () {
    int quads = (int)(xSize * ySize + xSize * zSize + ySize * zSize) * 2;
    int[] triangles = new int[quads * 6];
    mesh.triangles = triangles;
}

创建横向的三角方式与创建网格的做法相同。至此为止位置不同的是顶点在下一行的偏移相当全部的环形顶点之和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
private void CreateTriangles () {
    int quads = (xSize * ySize + xSize * zSize + ySize * zSize) * 2;
    int[] triangles = new int[quads * 6];
    int ring = (xSize + zSize) * 2; //计算环偏移
    int t = 0, v = 0;

    for (int y = 0; y < ySize; y++, v++) {
        for (int q = 0; q < ring - 1; q++, v++) {
            t = SetQuad(triangles, t, v, v + 1, v + ring, v + ring + 1);
        }
        t = SetQuad(triangles, t, v, v - ring + 1, v + ring, v + 1);
    }

    t = CreateTopFace(triangles, t, ring);
    t = CreateBottomFace(triangles, t, ring);
    mesh.triangles = triangles;
}

很不幸顶部与底部的面并不简单。顶点的布局就像是一个网格被环包围。

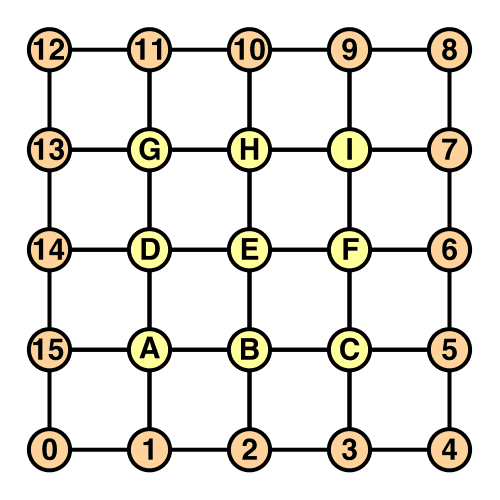
盖子就像在环里的网格

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
private int CreateTopFace (int[] triangles, int t, int ring) {
    int v = ring * ySize;
    for (int x = 0; x < xSize - 1; x++, v++) {
        t = SetQuad(triangles, t, v, v + 1, v + ring - 1, v + ring);
    }
    t = SetQuad(triangles, t, v, v + 1, v + ring - 1, v + 2);

    int vMin = ring * (ySize + 1) - 1;
    int vMid = vMin + 1;
    int vMax = v + 2;

    for (int z = 1; z < zSize - 1; z++, vMin--, vMid++, vMax++) {
        t = SetQuad(triangles, t, vMin, vMid, vMin - 1, vMid + xSize - 1);
        for (int x = 1; x < xSize - 1; x++, vMid++) {
            t = SetQuad(
                triangles, t,
                vMid, vMid + 1, vMid + xSize - 1, vMid + xSize);
        }
        t = SetQuad(triangles, t, vMid, vMax, vMid + xSize - 1, vMax + 1);
    }

    int vTop = vMin - 2;
    t = SetQuad(triangles, t, vMin, vMid, vTop + 1, vTop);
    for (int x = 1; x < xSize - 1; x++, vTop--, vMid++) {
        t = SetQuad(triangles, t, vMid, vMid + 1, vTop, vTop - 1);
    }
    t = SetQuad(triangles, t, vMid, vTop - 2, vTop, vTop - 1);

    return t;
}

private int CreateBottomFace (int[] triangles, int t, int ring) {
    int v = 1;
    int vMid = vertices.Length - (xSize - 1) * (zSize - 1);
    t = SetQuad(triangles, t, ring - 1, vMid, 0, 1);
    for (int x = 1; x < xSize - 1; x++, v++, vMid++) {
        t = SetQuad(triangles, t, vMid, vMid + 1, v, v + 1);
    }
    t = SetQuad(triangles, t, vMid, v + 2, v, v + 1);

    int vMin = ring - 2;
    vMid -= xSize - 2;
    int vMax = v + 2;

    for (int z = 1; z < zSize - 1; z++, vMin--, vMid++, vMax++) {
        t = SetQuad(triangles, t, vMin, vMid + xSize - 1, vMin + 1, vMid);
        for (int x = 1; x < xSize - 1; x++, vMid++) {
            t = SetQuad(
                triangles, t,
                vMid + xSize - 1, vMid + xSize, vMid, vMid + 1);
        }
        t = SetQuad(triangles, t, vMid + xSize - 1, vMax + 1, vMid, vMax);
    }

    int vTop = vMin - 1;
    t = SetQuad(triangles, t, vTop + 1, vTop, vTop + 2, vMid);
    for (int x = 1; x < xSize - 1; x++, vTop--, vMid++) {
        t = SetQuad(triangles, t, vTop, vTop - 1, vMid, vMid + 1);
    }
    t = SetQuad(triangles, t, vTop, vTop - 1, vMid, vTop - 2);

    return t;
}